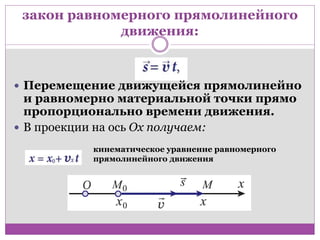
Движение объектов является одним из ключевых понятий в физике. Оно может происходить по разным законам, и каждый закон движения характеризуется определенной скоростью. В данной статье мы рассмотрим материальную точку, движущуюся вдоль оси Ox по закону х = 8t и поговорим о ее скорости.
Закон движения х = 8t означает, что положение точки (обозначим его как x) зависит от времени (обозначим его как t) и выражается линейной функцией. То есть, каждый момент времени t соответствует определенное значение положения x. Например, при t = 0, x = 0, при t = 1, x = 8 и так далее. Это означает, что материальная точка движется с постоянной скоростью 8 единиц длины в единицу времени.
Скорость материальной точки определяет, как быстро она меняет свое положение со временем. Для точки, движущейся по закону х = 8t, скорость является постоянной и равной 8 единицам длины в единицу времени. Это означает, что каждую секунду точка перемещается на 8 единиц в положительном направлении оси Ox.
Как определить скорость материальной точки, движущейся вдоль оси Ox по закону х = 8t
Для определения скорости материальной точки, движущейся вдоль оси Ox по закону x = 8t, необходимо использовать производную от функции x по времени. Производная функции x = 8t равна постоянной величине 8.
Таким образом, скорость материальной точки по оси Ox будет постоянной и равной 8 единицам длины в единицу времени. В данном случае единицей длины может быть, например, метр, и единицей времени — секунда. Таким образом, скорость будет равна 8 м/с.
| Величина | Значение | Единицы измерения |
|---|---|---|
| Скорость | 8 | м/с |
Таким образом, скорость материальной точки, движущейся вдоль оси Ox по закону x = 8t, составляет 8 метров в секунду.
О материальной точке
Движение материальной точки может быть описано с помощью нескольких параметров, включая положение, скорость и ускорение. В данном случае, материальная точка движется вдоль оси Ox по закону x = 8t, где x — координата точки вдоль оси Ox, а t — время.
Скорость материальной точки — это производная ее координаты по времени. В данном случае, скорость будет равна 8, так как координата меняется линейно с течением времени. Это означает, что материальная точка движется со st, постоянной скоростью в положительном направлении оси Ox.
Материальная точка — это важное понятие в физике, которое позволяет упрощенно описывать движение объектов, у которых размеры и форма не являются существенными. Это позволяет проводить анализ и решение физических задач с большей простотой и точностью.
О законе движения
Согласно этому закону, координата объекта изменяется пропорционально времени, с коэффициентом пропорциональности равным 8. Если время увеличивается, то координата растет, и наоборот, если время уменьшается, то координата уменьшается.
Такой закон движения может быть использован для определения скорости объекта. Скорость — это физическая величина, которая определяет изменение координаты объекта за единицу времени. В данном случае, скорость материальной точки можно найти как производную от уравнения движения по времени: v = dx/dt = 8, где v — скорость объекта.
Таким образом, данный закон движения позволяет определить координату объекта в зависимости от времени и вычислить его скорость.
Формула для расчета скорости
Для определения скорости материальной точки, движущейся вдоль оси Ox по закону х = 8t, можно использовать следующую формулу:
| Символ | Обозначение |
|---|---|
| х | Координата материальной точки в момент времени t |
| t | Момент времени |
| v | Скорость точки в момент времени t |
Для нахождения скорости нужно взять производную от заданного закона движения:
v = dx/dt
где dx — дифференциал координаты х, dt — дифференциал времени.
Подставляя закон движения х = 8t в формулу для скорости, получим:
v = d(8t)/dt
Раскрывая скобки и беря производную по времени, получаем:
v = 8
Таким образом, скорость материальной точки, движущейся по закону х = 8t, равна постоянной величине 8 и не зависит от времени.
Основные формулы физики
Ниже приведены некоторые из основных формул физики:
1. Формула скорости: v = s/t, где v — скорость, s — пройденное расстояние, t — время.
2. Формула ускорения: a = (v — u)/t, где a — ускорение, v — конечная скорость, u — начальная скорость, t — время.
3. Формула закона трения: F = μN, где F — трение, μ — коэффициент трения, N — сила нормального давления.
4. Формула закона Гука: F = kx, где F — сила, k — коэффициент упругости, x — деформация.
5. Формула энергии: E = mc², где E — энергия, m — масса, c — скорость света.
6. Формула закона всемирного тяготения: F = G(m₁m₂)/r², где F — сила гравитационного притяжения, G — гравитационная постоянная, m₁ и m₂ — массы двух тел, r — расстояние между ними.
Это лишь небольшой перечень основных формул физики. Физика позволяет нам понять и объяснить многое в мире, и формулы играют ключевую роль в этом понимании.
Применение формулы к заданному закону движения
Применяя эту формулу к заданному закону движения, найдем скорость точки:
? = ??/??
Подставив значение ? = 8?, получим:
? = ?(8?)/??
Производная от времени константы равна нулю, поэтому получаем:
? = 8
Таким образом, скорость материальной точки, движущейся вдоль оси ?? по закону ? = 8?, равна 8 единицам длины в единицу времени.
Примеры расчетов скорости
Для материальной точки, движущейся вдоль оси Ox по закону х = 8t, можно рассчитать скорость в различные моменты времени.
- Пусть t = 1 секунда. Тогда х = 8 * 1 = 8 м. Скорость в этот момент времени будет равна производной от х по t, то есть скорости изменения позиции: v = dx/dt. В данном случае v = d(8t)/dt = 8 м/с.
- Пусть t = 2 секунды. Тогда х = 8 * 2 = 16 м. Аналогично, скорость в этот момент времени будет равна производной от х по t: v = d(8t)/dt = 8 м/с.
- Пусть t = 0.5 секунды. Тогда х = 8 * 0.5 = 4 м. Скорость в этот момент времени будет равна производной от х по t: v = d(8t)/dt = 8 м/с.
Таким образом, видно, что скорость материальной точки, движущейся вдоль оси Ox по закону х = 8t, всегда равна 8 м/с.
Пример 1: t = 2 сек
Для примера возьмем момент времени, равный 2 секундам. Подставив это значение в выражение закона движения х = 8t, получим:
х = 8 * 2 = 16 м
Таким образом, при значении времени t = 2 секунды, материальная точка находится на расстоянии 16 метров от начала координат. Также можно вычислить скорость точки в этот момент времени, зная, что производная от закона движения по времени t равна скорости:
v = dx/dt = d(8t)/dt = 8 м/с
То есть в момент времени t = 2 секунды скорость материальной точки равна 8 м/с.
Пример 2: t = 5 сек
Рассмотрим скорость материальной точки, движущейся вдоль оси Ox по закону х = 8t, в момент времени t = 5 сек.
Подставив t = 5 сек в выражение х = 8t, получим:
х = 8 * 5 = 40 м
Таким образом, в момент времени t = 5 сек скорость материальной точки составляет 40 м/с.
Вопрос-ответ:
Как определить скорость материальной точки?
Скорость материальной точки определяется как производная от ее координаты по времени. Для точки, движущейся по оси Ox по закону x = 8t, скорость будет равна 8.
Как изменяется скорость материальной точки в данном случае?
Скорость материальной точки, движущейся по оси Ox по закону x = 8t, остается постоянной и равной 8. Это значит, что точка движется с постоянной скоростью.
Что такое производная? Как она связана со скоростью материальной точки?
Производная — это понятие математического анализа, которое позволяет найти изменение одной величины относительно другой. В данном случае, производная от координаты точки по времени позволяет найти скорость точки. В примере с точкой, движущейся по оси Ox по закону x = 8t, значение производной равно 8, что соответствует скорости точки.
Может ли скорость материальной точки изменяться, если она движется по прямой вдоль оси Ox?
Если материальная точка движется по прямой вдоль оси Ox без изменения направления и постоянной скоростью, то значение ее скорости будет оставаться неизменным на протяжении всего движения.